Kaifa Luo

I obtained my Ph.D. in Physics from UT Austin in 2025, where I was advised by Feliciano Giustino. I earned an M.S. in Computational Science, Engineering, and Mathematics from the Oden Institute in 2024. Earlier, I studied at Wuhan University in China, and worked at HKUST under the supervision of Xi Dai.

Email / Scholar

Research

My research interests span many-body physics and first-principles methodologies for real systems,
and lie at the intersection of quantum materials, quantum geometry, and quantum optics,
aiming to design and control functionalities for information and energy applications.

Selected papers with highlights:

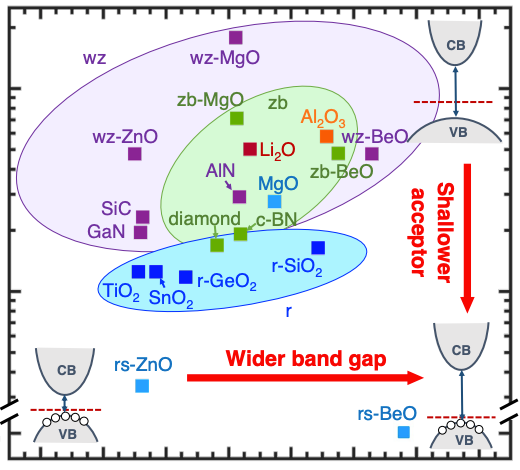
	Extreme-Band-Gap Semiconductors with Shallow Dopants and Mobile Carriers Sieun Chae, Nocona Sanders, Kelsey A. Mengle, Amanda Wang, Xiao Zhang, Jon Lafuente Bartolome, Kaifa Luo, Yen-Chun Huang, Feliciano Giustino, John T. Heron, Emmanouil Kioupakis arXiv:2506.07284, 2025 TBD.
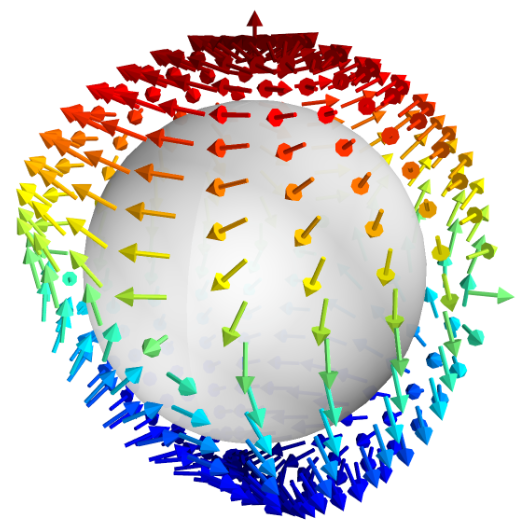
	Symmetry-protected topological polarons Kaifa Luo, Jon Lafuente-Bartolome, Feliciano Giustino submitted, 2025 Combining group-theoretic analysis and state-of-the-art first-principles calculations, we classified and proposed polarons with integer topological charges in oxides and nitrides.
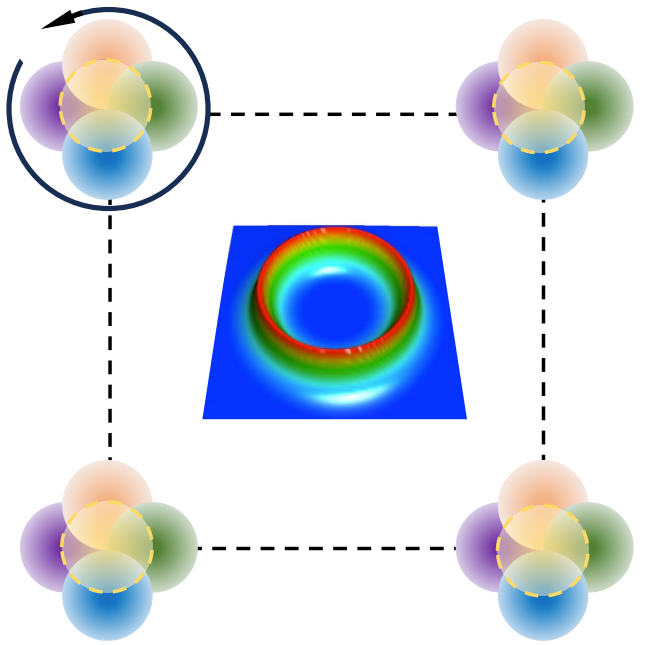
	Incommensurate Transverse Peierls Transition and Signature of Chiral Charge Density Wave in EuAl₄ FZ Yang^, KF Luo^, Weizhe Zhang, Xiaoyu Guo, WR Meier, H Ni, HX Li, P Mercado Lozano, G Fabbris, AH Said, C Nelson, TT Zhang, AF May, MA McGuire, R Juneja, L Lindsay, HN Lee, J-M Zuo, MF Chi, X Dai, Liuyan Zhao, H Miao Nature Communications 16, 10401, 2025 TBD.
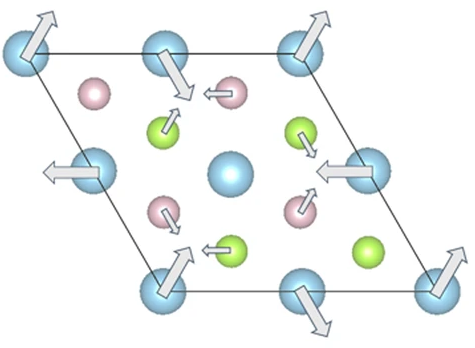
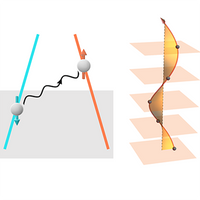
	Understanding chiral charge-density wave by frozen chiral phonon Shuai Zhang, Kaifa Luo^†, Tiantian Zhang^† npj Computational Materials 10 (1), 264, 2024 By tracing electron-phonon interactions in a chiral charge-density wave, we sugguested symmetry-selective engineering to control chirality in low-dimensional quantum materials.
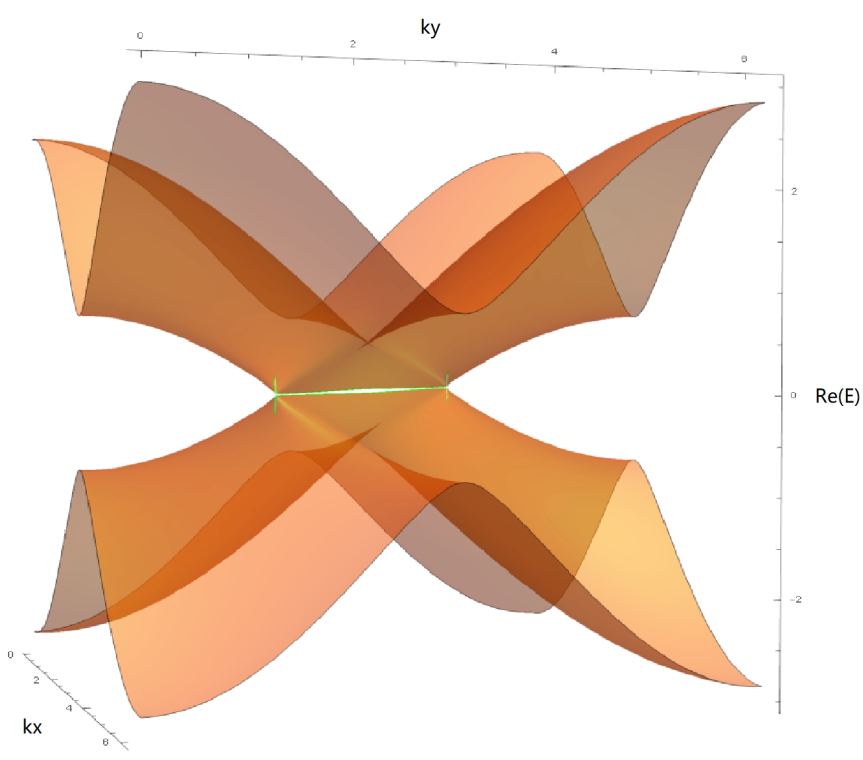
	Transverse Peierls transition Kaifa Luo, Xi Dai Physical Review X 13 (1), 011027, 2023 By condensating transverse phonons via selection rules of angular momentum, we proposed novel density-wave states in topological semimetals.
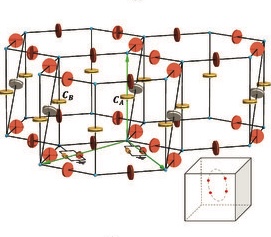
	Non-Hermitian honeycomb lattice: nodal manifolds bounded by exceptional points Kaifa Luo, Jiajin Feng, YX Zhao, Rui Yu arXiv 1810.09231, 2018 Non-Hermiticity of Hamiltonian brings complex behaviors to spectrum and dynamics. By designing a proof-of-principle electric lattice with gain and loss, we studied spectra evolution of a non-Hermitian topological semimetal.
	Topological nodal states in circuit lattice Kaifa Luo, Rui Yu, Hongming Weng Research, 2018 Topological band theory can be applied to any periodically coupled harmonic oscillators. Guided by this idea, we designed topological nodal structures in a LC circuit lattice.

Feel free to steal this website's source code, which is originated from Leonid Keselman's Jekyll fork of this page.